Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance,[1] one arrives at the usual mathematical equation that describes this relationship:[2]
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm's law states that the R in this relation is constant, independent of the current.[3]
The law was named after the German physicist Georg Ohm, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above (see History section below) to explain his experimental results. The above equation is the modern form of Ohm's law.
In physics, the term Ohm's law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:
where J is the current density at a given location in a resistive material, E is the electric field at that location, and σ is a material dependent parameter called the conductivity. This reformulation of Ohm's law is due to Gustav Kirchhoff
In circuit analysis, three equivalent expressions of Ohm's law are used interchangeably:
The interchangeability of the equation may be represented by a triangle, where V (voltage) is placed on the top section, the I (current) is placed to the left section, and the R (resistance) is placed to the right. The line that divides the left and right sections indicate multiplication, and the divider between the top and bottom sections indicates division (hence the division bar).
Resistive circuits
Resistors are circuit elements that impede the passage of electric charge in agreement with Ohm's law, and are designed to have a specific resistance value R. In a schematic diagram the resistor is shown as a zig-zag symbol. An element (resistor or conductor) that behaves according to Ohm's law over some operating range is referred to as an ohmic device (or an ohmic resistor) because Ohm's law and a single value for the resistance suffice to describe the behavior of the device over that range.Ohm's law holds for circuits containing only resistive elements (no capacitances or inductances) for all forms of driving voltage or current, regardless of whether the driving voltage or current is constant (DC) or time-varying such as AC. At any instant of time Ohm's law is valid for such circuits.
Resistors which are in series or in parallel may be grouped together into a single "equivalent resistance" in order to apply Ohm's law in analyzing the circuit. This application of Ohm's law is illustrated with examples in "How To Analyze Resistive Circuits Using Ohm's Law" on wikiHow.
Reactive circuits with time-varying signals
When reactive elements such as capacitors, inductors, or transmission lines are involved in a circuit to which AC or time-varying voltage or current is applied, the relationship between voltage and current becomes the solution to a differential equation, so Ohm's law (as defined above) does not directly apply since that form contains only resistances having value R, not complex impedances which may contain capacitance ("C") or inductance ("L").Equations for time-invariant AC circuits take the same form as Ohm's law, however, the variables are generalized to complex numbers and the current and voltage waveforms are complex exponentials.[26]
In this approach, a voltage or current waveform takes the form
 , where t is time, s is a complex parameter, and A is a complex scalar. In any linear time-invariant system, all of the currents and voltages can be expressed with the same s
parameter as the input to the system, allowing the time-varying complex
exponential term to be canceled out and the system described
algebraically in terms of the complex scalars in the current and voltage
waveforms.
, where t is time, s is a complex parameter, and A is a complex scalar. In any linear time-invariant system, all of the currents and voltages can be expressed with the same s
parameter as the input to the system, allowing the time-varying complex
exponential term to be canceled out and the system described
algebraically in terms of the complex scalars in the current and voltage
waveforms.The complex generalization of resistance is impedance, usually denoted Z; it can be shown that for an inductor,
This form of Ohm's law, with Z taking the place of R, generalizes the simpler form. When Z is complex, only the real part is responsible for dissipating heat.
In the general AC circuit, Z varies strongly with the frequency parameter s, and so also will the relationship between voltage and current.
For the common case of a steady sinusoid, the s parameter is taken to be
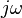 , corresponding to a complex sinusoid
, corresponding to a complex sinusoid  .
The real parts of such complex current and voltage waveforms describe
the actual sinusoidal currents and voltages in a circuit, which can be
in different phases due to the different complex scalars.
.
The real parts of such complex current and voltage waveforms describe
the actual sinusoidal currents and voltages in a circuit, which can be
in different phases due to the different complex scalars.Linear approximations
See also: Small-signal modeling and Network analysis (electrical circuits)#Small signal equivalent circuit
Ohm's law is one of the basic equations used in the analysis of electrical circuits. It applies to both metal conductors and circuit components (resistors)
specifically made for this behaviour. Both are ubiquitous in electrical
engineering. Materials and components that obey Ohm's law are described
as "ohmic"
which means they produce the same value for resistance (R = V/I)
regardless of the value of V or I which is applied and whether the
applied voltage or current is DC (direct current) of either positive or negative polarity or AC (alternating current).In a true ohmic device, the same value of resistance will be calculated from R = V/I regardless of the value of the applied voltage V. That is, the ratio of V/I is constant, and when current is plotted as a function of voltage the curve is linear (a straight line). If voltage is forced to some value V, then that voltage V divided by measured current I will equal R. Or if the current is forced to some value I, then the measured voltage V divided by that current I is also R. Since the plot of I versus V is a straight line, then it is also true that for any set of two different voltages V1 and V2 applied across a given device of resistance R, producing currents I1 = V1/R and I2 = V2/R, that the ratio (V1-V2)/(I1-I2) is also a constant equal to R. The operator "delta" (Δ) is used to represent a difference in a quantity, so we can write ΔV = V1-V2 and ΔI = I1-I2. Summarizing, for any truly ohmic device having resistance R, V/I = ΔV/ΔI = R for any applied voltage or current or for the difference between any set of applied voltages or currents.

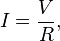

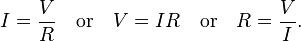
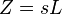

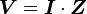
No comments:
Post a Comment